Bachelor's Thesis in Electrical Engineering
by Niklas Lissjos
This thesis provides an insight into photovoltaics energy system design and simulation. The report describes each step along the design path for an electrical system for off-grid use. Solar power feasibility at northern latitudes has been a focus, and a supplied case study using solar irradiation data courtesy of the European Organization for the Exploitation of Meteorological Satellites. Because this study covers an off-grid system, it means a battery-bank is part of the design. System simulations are performed for the case study, located in Norway. Based on a winter-optimized design and component efficiency factors, it is concluded feasible with the help of a relatively large PV array. When designing a PV energy system, there can be different practical limitations present. Therefore, alternative methods are needed. In parallel with the design process, a simple web application is developed as a tool and resource for this field of technology.
I would like to thank my supervisor Prof. Karl Skretting, at the University of Stavanger, who has provided helpful guidance and discussions along the way. And a special thanks to Daniel Philipp at Germany's National Meteorological Service, the Deutscher Wetterdienst, who has given helpful advice and guidance during the irradiation data extraction and evaluation process.
Stavanger, Spring 2020
Niklas Lissjos
| CDN | Content Delivery Network |
| CMSAF | Satellite Application Facility on Climate Monitoring |
| CSS | Cascading Style Sheets |
| DOD | Depth Of Discharge |
| GUI | Graphical User Interface |
| HTML | Hypertext Markup Language |
| EM | Electromagnetic |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| MPP | Maximum power point |
| MPPT | Maximum power point tracking |
| NREL | National Renewable Energy Laboratory |
| OCV | Open Circuit Voltage |
| PHP | Hypertext Preprocessor |
| PVGIS | Photovoltaic Geographical Information System |
| PV | Photovoltaic |
| PWM | Pulse width modulation |
| SCC | Short Circuit Current |
| SSH | Secure Shell |
| STC | Standard Test Conditions |
| SOC | State Of Charge |
| SZA | Solar Zenith Angle |
"Energy is the only universal currency: one of its many forms must be transformed to another in order for stars to shine, planets to rotate, plants to grow, and civilizations to evolve."
– Vaclav Smil
Photovoltaic energy is the electric energy obtained by capturing and absorbing photons given off by the sun to the earth's surface. This way of generating electrical power is based on the photovoltaic (PV) effect. It is done using photovoltaic cells that are produced using advanced semiconductor technology. The thesis is focused on the field of off-grid photovoltaic systems, meaning an electrical system that has energy storage and is independent of the electric power grid. This is sometimes called a stand-alone system.
The project aims to present an organized way of system design and evaluation of the main components, as well as making use of meteorological radiation data for the purpose. The report presents a step-by-step method where a case study is used to form an example. This case study is a fictionalized small house with relatively low energy demands, located in Stavanger, Norway. The report is not meant to be a complete design guide but to give an insight into analyzing feasibility, efficiency, and losses. Neither does the thesis aim to cover the economic aspects of solar energy, but rather the technological side. The minimum energy usage requirements of the case study house are mapped and based around this, a study on the feasibility of solar power at northern latitudes is formed. Because the winter weather and sun conditions, at the specific location, are the most challenging, this is a focus throughout the design. A battery bank is being sized based on capacity requirements and component losses. Solar radiation charging capabilities are based on meteorological data statistics. The amount of energy converted by the PV modules is evaluated based on factors such as optimal angle, temperature, and PV module conversion efficiency. The system component sizes and efficiencies found are merged into Python code for simulations. The designed system is simulated to test, verify, and draw conclusions. A simple web application is developed as a tool for some of the steps along the way.
The production of clean energy is of major importance today and in the future. Sustainable living and environmental consciousness are becoming a more significant part of each and everyone's lives. The thesis topic and objective is chosen and formulated based on an interest in sustainable energy generation for the future and off-grid living technologies. The steps described in the report are aimed at hobbyists or engineers interested in designing efficient photovoltaic systems without blindly trusting available solar energy kits. For homeowners wanting to "go solar", efficiency numbers are most likely not as important as the cost per watt output. However, for someone to purposely find appropriate components and an accurate cost per watt output, it is crucial to understand how the different system components performes under different weather conditions.
This chapter summarizes the theoretical background needed to work through and understand the methods and results presented later in this report. A focus is on solar radiation energy conversion and how the obtained energy can be stored. The chapter also includes some theory on energy consumption, and other components needed to design a complete system.
Power, P, SI unit Watt [W] or Joules per second [Js−1]
Electrical power [W]: The rate of performing work, or electrical energy transferred per unit time.
[W] & [VA]: These two units of power referes to real power and apparent power. Volt ampere [VA] is used to specify apparent power, when dealing with AC and reactive elements. Reactive elements is anything that has inductance or capacitance. Kilowatt [kW] represents real power, which per definition comes from resistive elements. Almost all electrical equipment, cables etc. has more or less inductive and capacitive elements, but only when using AC it will cause apparent power. [VA] specifications is therefore found for inverters and AC loads.
Energy, E, SI unit joules [J].
Electrical energy: Potential energy stored in, or due to electric
fields. Defined as power over a certain time and is denoted in watthours.
[Wh].
Energy can be found by integrating the continous power over time as follows:
Electrical charge, Q, SI unit coulombs [C].
1 [C] is defined as 1 ampere transferred during 1 second. More commonly denoted in ampere-hours, [Ah]. The relation between Ah and C is: 1[Ah] = 3600[C]
Publicly available radiation data from various online sources can be used for the dimenzioning of a PV powered electrical system.
The Satellite Facility on Climate Monitoring (CM SAF) based in Germany and Belgium, is an integral part of the European Organization for the Exploitation of Meteorological Satellites (EUMETSAT) . CM SAF develops, generates, and distributes satellite-derived solar energy-related data products. The data, holding various specifications and parameters can be ordered(free of charge) through their web user interface, and comes in the fileformat Tape Archive (TAR , also referred to as tarball). The files can be downloaded or sent other ways. The data from CM SAF can be analyzed in several different ways, but using R and the RStudio tool called "the CM SAF R Toolbox" provided by CM SAF, the file can be prepared, analyzed and visualized. This data has good geographical coverage and contains many useful parameters .
As radiation data is available as different parameters with various specifications, there is some background knowledge needed to be able to find, understand and make use of the appropriate data.
Energy from the sun, in the form of electromagnetic (EM) radiation, is carried by photons to the earth's surface. Photons is particles of light that is characterized by a wavelength (λ). Photon energy can be denoted in joules [J] or electron-volts [eV], where electron-volts is the energy recovered in the photovoltaic semiconductor technology . $$\label{ph_energy_j} E = \frac{hc}{\lambda}[J] = \frac{1.24}{\lambda}[eV]$$
h, is the Planck constant, 6.626 ⋅ 10−34 [kgm2s−1]
c, is the speed of light 2.998 ⋅ 108 [ms−1]
1 [eV] = 1.602 ⋅ 10−19 [J]. The energy required to raise an electron through 1 volt is 1.602 ⋅ 10−19 joules .
The wavelength λ, is denoted in micrometer [μm], and the different wavelength's make up the light spectrum that travels to earth.
Energy from the sun, in the form of convection, and naturally occuring radiation, is at all times reaching the earth. Below, is a summary of definitions needed further in this section, to understand how this radiation behaves when entering and passing through the atmosphere .
Solar radiation: Electromagnetic energy radiated by the sun.
Solar irradiation: The amount of radiation that is absorbed by a surface on the earth. Power per unit area which is commonly denoted in watts per squaremeter, [Wm−2]
Direct beam solar radiation: Solar radiation that reaches the earth's surface without being diffused.
Diffuse solar radiation: The solar radiation that is absorbed, reflected or scattered when passing through the atmosphere.
Reflected solar radiation: The solar radiation that is reflected by a surface.
Global solar radiation: The sum of direct, diffuse and reflected solar radiation.
Solar spectrum: The range of wavelengths that the sun radiates.
Zenith: An imaginary line perpendicular to the earth surface at the point of interest (on earth), pointing up in the sky.
Solar zenith angle, SZA or θZ: The angle between the zenith and the line to center of the sun.
The full EM spectrum from the sun is the assemble of different EM radiations , such as Gamma-ray, Ultraviolet (UV), and Microwaves. Still, not all solar radiation is useful with photovoltaics .

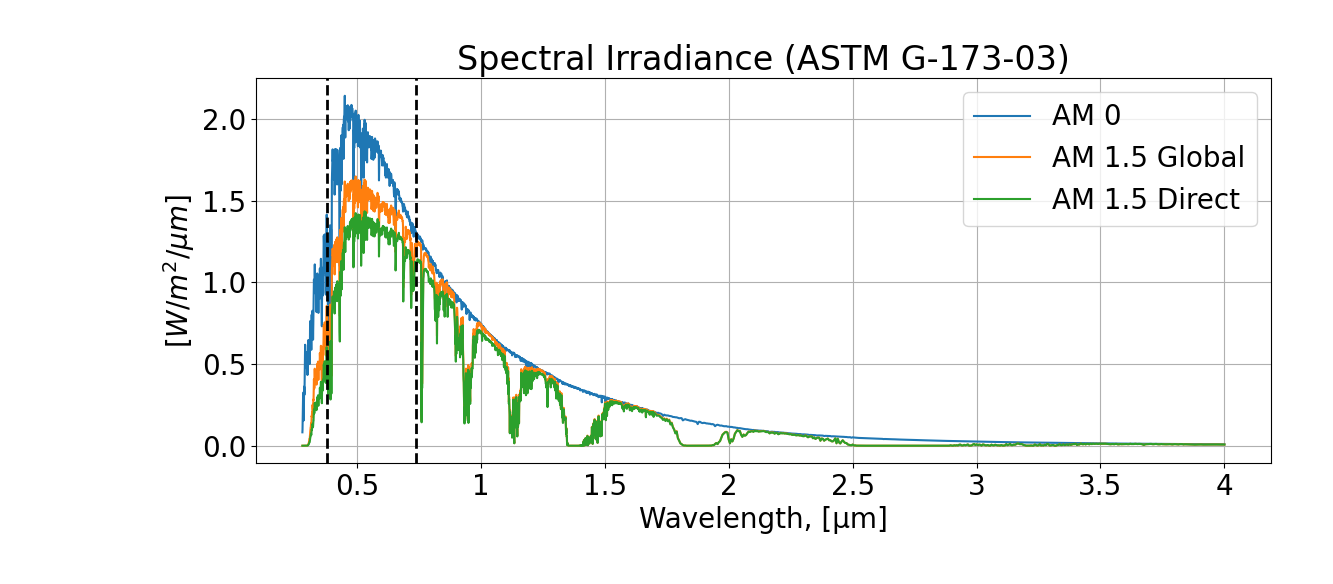
The energy for each wavelength that reaches the earth is just a fraction of what is being radiated and consists roughly of Infrared(IR), visible light, and Ultraviolett(UV). The dotted lines in figure 2.1 indicate roughly where these three different radiation types meet. The middle section shows the visible light and composes 44 percent of the energy reaching the earth's surface. The left part at only 9 percent of received energy is the UV light. The right section is IR, which at 47 percent is the most significant fraction of energy reaching the earth .
The AM parameters seen in figure 2.1 is short for Air mass. AM is a ratio of lenght parameter that describes the distance travelled by the sun rays, from entering the atmosphere til reaching the earth surface . $$\label{am} \textrm{Air mass, AM} = \frac{\textrm{Path length traveled}}{\textrm{Vertical depth of the atmosphere}}$$ When the pathlength travelled is the shortest, AM equals 1, and that is when the sun rays is perpendicular to the earth surface. As in most cases, the sun rays will have an angle through the atmosphere, causing a longer path length. In some places at noon, AM equals approximately 1 in summer and 2 in the winter. This will differ largely between different latitudes, and generally we get more scattering and more losses at higher latitudes beacuse of the longer path length . AM can be calculated using cosine of the SZA(θZ) as seen in equation [am2] . $$\label{am2} AM = \frac{1}{cos(\theta_{Z})}$$ AM 0 is extraterrestrial, and is used in space applications. As part of Standard Test Conditions (STC), AM 1.5 is being used as an industry standard for computations and to state PV module nominal capacities. Using 1.5 AM gives a way of setting a standard of fixed light spectrum, giving a simulated atmosphere during laboratory testing. More about STC in section 2.2.3 .
ASTM G-173-03 is a standard that forms a terrestrial (on earth) solar spectral irradiance distribution . It also defines a set of specified atmospheric reference conditions for evaluations in PV. This standard was founded by the American Society for Testing and Materials (ASTM) in conjunction with the PV industry and US government laboratories .
Below is a brief summary of definitions and useful radiation parameters that is available in satellite derived data from CMSAF and others.
Irradiance:
Solar spectral irradiance (SSI): The power (radiant flux) received by the outer atmosphere (AM 0) in a unit surface area for a specified wavelength interval (dλ), with the units [Wm−2μm−1] . See AM 0 in figure 2.1.
Irradiance: The integral of the spectral irradiance extended to all wavelengths of interest. With the units watts per square meter: Looking back at figure 2.1, this would correspond to the area under one curve. $$\label{irr_int} \textnormal{Irradiance}, I = \int_{0}^{\lambda}P(\lambda)d\lambda$$ [2.6] where P(λ) is the spectral power density.
Shortwave Incoming Solar Radiation (SIS): The irradiance reaching earth on a horizontal surface, in the wavelength range of 0.2 to 4 μm. In theory the result from an integral like equation [irr_int], with the units watts per square meter. Commonly, high-resolution SIS data is achieved from satellite-derived values where it is calculated as below . $$\textnormal{SIS = (1 - CAL)} \cdot \textnormal{SIS_clear_sky}$$ [2.7] where, CAL is the Effective Cloud Albedo. A higher CAL value indicates that clouds reflect a larger amount of solar radiation. SIS_ clear_ sky is the surface solar irradiance if no clouds. SIS data can often be acquired as daily, monthly or yearly averages. The SIS parameter therefore gives a good value for further PV calculation, involving the different effecting factors we have on the ground .
Spectrally resolved irradiance (SRI): Another type of irradiance parameter often available from satellite monitoring. SRI data contain the spectrally resolved shortwave radiation, where the spectrum is split up into small wavelength bands. This parameter is therefore similar to SIS but separated into discrete wavelength bands. SRI data can be numerically integrated to output SIS, or the spectrum of interest .
Radiation:
Units of energy that can be found by taking the time integral of the irradiance extended over a given period of time. Radiation data can for example be found in kilowatthours per squaremeter per day .
To absorb and convert photon energy, PV cell technology is being used. The PV cell can be manufactured using different techniques and is usually produced using Silicon (Si). Monocrystalline and Polycrystalline silicon cell technology is the two most commonly used in currently available modules. Very shortly described the PV cell is built up of silicon and the electric current occurs at a pn-junction. P and N-type silicon is produced by doping the materials. A PN-junction is then made up of these two doped materials. An electric field occurs between the P and N part when photons from the sun reach the PN-junction. And from this, electron hole pairs occurs. A voltage will develop across the PN-junction when the incident radiation and photon energy exceeds the bandgap energy . To summarize the production of the PV cell semiconducting material, the main steps is explained below. From Quartzite rock, metallurgical silicon is produced through several steps and processes, where finally the silicon is purified through melting. At this stage the material can be used to various applications not only for the semiconductor industry .
Next phase is the production of polycrystalline silicon rods through another melting and purifying process. At this point, silicon wafers can be produced from the silicon rods. The wafers is obtained by sawing the rods using a wire saw technique, followed by refining steps such as polishing .
Or, multi/monocrystalline ingots can be produced, through a process where one single crystal of silicon is made, as opposed to polycrystalline which is essentially made from many silicon fragments melted together. This second step can generally make the monocrystalline cell more expensive but in return, more efficient .
Looking at operational characteristics of the PV cell, it is known that the bandgap energy varies from material to material but silicon needs approximately 1.11 [eV] . Wavelength (λ), smallar then about 1.1 μm will uphold the energy required for silicon-based PV cells. Looking at figure 2.1 we can see that these wavelengths is in the near IR range and below. This means that PV cells can absorb and convert energy with wavelengths in the range of approximately 0.2 to 1.1 μm .
Even though there are different manufacturing techniques and semiconductor metallurgy, the main characteristics of most PV cells can be modelled and approximated by the below ideal cell equivalent circuit. This can help to evaluate different situations and understand characteristics. By using this circuit model, it is possible to work with Kirchoff's circuit law's and derive formulas for testing and understanding .
(0,0) to[isource = Iph] (0,3) to[short, -*] (3,3) to[short, -*] (6,3) (3,3) to[diode, i>_=ID] (3,0) – (0,0) (3,3) – (6,3) to[resistor = Rsh, i>_=IRsh] (6,0) – (3,0) (6,3) to[resistor = Rs, i>_=I] (12,3) to[short, o-*] (12,3) node[anchor=west]+ (6,0) – (12,0) to[short, o-*] (12,0) node[anchor=west]-;
Current source Iph represents the photovoltaic effect of light intensity on the cell. The more sunlight available, the more current will flow .
The diode will model how the cell operates without sunlight present .
Shunt resistance Rsh occurs from imperfections in the semicondutor material which under different conditions presents alternative paths for the current. Can be seen as "leaks" around the edges of the semiconductor .
Series resistance RS comes mainly from three places. It is some resistance when current moves through the semiconductor material, the interface/contact where the metal contacts connect to the semiconductor material, and in in the metal contacts themselves .
By using Kirchoff's current law's, ideal circuit element equations and ohms law, the below characteristic equation describing the PV cell output current is found . $$I = I_{ph} - I_S \Big(e^{(\frac{V_D}{nV_T})}-1\Big) - \frac{V + IR_{s}}{R_{SH}}$$
IS is the reverse saturation current as normally seen in the Shockley diode equation.
n is the diode ideality factor. Ideally n = 1.
VT is the thermal voltage. $V_{T} = \frac{kT}{q}$, where k is the Boltzmann constant, T for temperature and q = electron charge. VT≈ 0.0259 volts at $25°$C .
Output voltage V is across the PV cell +/- terminals.
Based on the ideal cell circuit in figure [cell_equivalent], it is evident that, to get the most out of this circuit it required for RS to have zero resistance and Rsh to have infinite resistance. Disregarding the resistors, imagining no sunlight available, the PV cell acts as a diode. And when the cell receives radiation from the sun, the current Iph appears as illustrated in figure 2.2. The part of the irradiated curve inside the green rectangle are what is usually seen up-side-down, as shown in figure 2.3 .
Looking back at the equivalent circuit in figure [cell_equivalent], it is a fact that the current Iph, will be the biggest when the cell is shorted without load, i.e. load voltage is zero. Iph will on the other hand be zero when no load is connected, and the open-circuit voltage VOC is then at its biggest. This results in: ISC = − Iph, and the IV curve is plotted as shown in figure 2.3 .
Because power is defined as P = U x I, there will be a specific point on the IV curve where power (P) is the biggest. This point is called the Maximum power point (MPP). This is visualized in figure 2.3 by the gray marked area that would represent power. MPP on the IV-curve, will be where this gray "power area" is the biggest possible . The real IV-curve for a PV cell or module is found in laboratories under Standard test conditions (STC), as explained in section 2.2.3.
To get the most power out of a PV cell, it needs to be forced to work at the MPP. Since the cell and the IV-curve will constantly vary from factors such as temperature and irradiance, the MPP will also change as a result. By connecting a load directly to a cell or module this would not operate very efficiently, but instead this is solved and handled using a technique called Maximum power point tracking(MPPT), which is handled by a charge controller . Besides MPPT, the cell temperature is a factor that affects the efficiency remarkably. Voltage drops from increasing internal resistance at higher cell temperatures, and current increases very little, therefore resulting in a power loss . For the entire PV module, there will be more factors to consider, such as soiling and shading. More about this in section 2.2.3.
PV modules or solar panels as the modules are commonly called, is built up by a number of PV cells to output a certain voltage. In PV powered systems, a number of PV modules is connected and together forms a PV array that can supply the system with power.
Or shortly called STC, is an industry-standard for the conditions where PV Modules is being tested and rated in laboratories. Thanks to this standard of test conditions, modules can be accurately compared. The STC consists of the following three criteria that is used during laboratory testing :
Irradiance(artificial) of 1000 [Wm−2]
Cell temperature of 25[C]
Air mass: 1.5 AM
Using the STC, PV module manufacturers can test and declare a number of electrical properties. These data can be found on the product datasheet. Since the STC is a controlled testing environment, the parameters has fixed values under STC .
MPP voltage [Vmpp], is the voltage found under STC, where the module outputs the most power.
MPP current [Impp], is the current found under STC, where the module outputs the most power.
Watt-peak [Wp], is the nominal power output under STC, based on Vmpp and Impp. This is the value that is commonly advertised as the module output.
Module efficiency [%], tells how big part of the suns power that can be converted to electrical power. Common values ranges from 15 to 23 percent. It is found as follows : $$\textnormal{PV module efficiency, }\eta_{mpp} = 100\% * \Bigg(\frac{P_{MPP}}{P_{sunlight}}\Bigg)$$ Where, Psunlight is 1000 watts per square meter, under STC.
Beyond STC parameters, manufacturers declare physical dimensions, characteristic curves, a nominal operating temperature and electrical properties under the nominal temperature. A tempererature coefficient of power is declared in percent per degree celcius. This is a coefficient stating how big loss to expect per degree celsius change. The coefficient is negative since efficiency goes down with increasing temperature .
A shaded or mismatched cell in a module behaves like "a clog in the pipe", as resistivity will go up and make the current drop. Other than shading, this phenomenon can also be caused by soiling, aging or other damage to a cell or module. A cell that gets raised resistance like this, also heats up quickly, which will result in degraded performance of that cell. The solution to this is bypass-diodes. This can be an issue at cells in a module, but also in a string of modules when parts of a module gets shaded. To avoid this problem as much as possible, bypass-diodes is integrated in PV modules, and it can be added to the strings in a solar array.
The PV module configuration of cells, and use of bypass-diodes can be found from the product datasheet. For example, a 60 cell module has three built in bypass diodes that can each bypass a string of 20 cells in the module . These different factors discussed above will cause a loss that is very hard to set up a general number or equation for. Shading over large areas of a PV array will have a big impact and can quickly halve the output. This is simply a thing that needs to be avoided in order to achieve a system as efficient as possible. According to NREL, soiling, shading, and cell mismatch often cause 2 to 3 percent losses .
Established definitions and parameters used for the topic has been summarized below:
Meridian: Lines that passes between south/north pole parallel to the prime meridian. The prime meridian, also called the Greenwich meridian, since it is passing through Greenwich.
Longitude: Measure distance in degrees, east or west of the prime meridian. The prime meridian is defined to be the 0 degree longitude, with plus/minus 180 degrees, all longitudes covers the earth.
Equator: Is in the center of earth in relation to its rotational axis, defined as 0 degree latitude, with plus/minus 90 degrees covering the earth between south/north pole.
Latitude: Positive degrees counted from the equator towards the north pole, and vice versa towards the south pole.
Solar noon: At a specific location, the time where the sun reaches the highest position in the sky, meaning the sun crosses the meridian the location. Solar noon occurs at different hours at different locations since the earth rotational axis is tilted 23.5$°$, in relation to a perpendicular line with the sun .
Solar altitude angle: The suns angular height in relation to the horizontal. 0 degress at sunrise/sunset and at most 90 degrees at solar noon. .
Module elevation angle, θ: The angle of which the PV module is tilted in relation to the horizontal.
Module azimuth angle: The angle of which the PV module is rotated along the horizon, in relation to the equator. Also called the compass direction.
Declination angle: The angle of which the earth rotational axis is tilted in relation to a perpendicular line towards the suns center. See figure 2.8.
June and December solstice: The time of year where the sun is either at its largest or smallest altitude angle. The suns biggest altitude angle of the year is June 21, and the least on December 21.
True south: The heading from any point on earth, towards the south pole.
Equinox: When the motion of the sun crosses the equator
The earth rotates around its axis once per day, as well as orbiting in an elliptical path around the sun ones during a year, as shown in figure 2.8. Because of the earth's tilted axis in relation to the sun, the declination angle δ appears. This angle varies between 23.45$°$ in the summer, and -23.45$°$ in the winter .
There is two angles of the PV module that needs to be considered when planning an optimal mounting position. The elevation angle (θ), and the azimuth angle, as shown in figure 2.9.
An alternative to mounting the module or array in a fixed position is to use a solar tracker. One or two axis, solar trackers, is a piece of equipment that makes the module/array automatically follow the sun for optimal irradiation absorption. The two-axis tracker adjusts both elevation and azimuth, whilst the one axis tracker, is slightly simpler and changes only the azimuth angle. Solar tracking maximizes the intersection with the sun's rays. Figure 2.10 illustrates the cosine to angle relation, that dictates the sun rays radiation components that can be absorbed by the PV module .
The gain from using a solar tracker versus a fixed position depends on many factors. In Photovoltaics Systems Engineering , it is stated that two-axis tracking in a desert climate, can help achieve up to 50 percent more energy during summer and 20 percent during winter in best-case scenarios. But locations affected by more diffuse solar radiation such as Seattle WA, would gain 35 percent in summer and only 9 percent in winter time. It is also stated that a PV module can have an azimuth angle offset from the solar noon of up to 22.5 degrees, with no more than a 2 percent irradiation loss. Common in smaller installations is to use a fixed position where the aim is to find the optimal angles, for most possible irradiation absorbance .
The illustration in figure 2.8 explains why the declination angle δ will have a sinusoidal behavior. During summer in the northern hemisphere, it will alternate between $23.45°$ and $0°$, and similarly, in winter it will alternate between $-23.45°$ and $0°$. The average seasonal declination angle is found using the same method, as when finding an average sinusoidal voltage output, 2A/π, wherein this case, the amplitude is the declination degrees. Resulting in: $2\cdot-23.45° / \pi \approx -14.93 °$, which is average angle for wintertime. Based on this, it is common practice to set the optimal PV module elevation angle as follows:
For best average winter performance, elevation angle = (latitude + 14.93)
For best average summer performance, elevation angle = (latitude − 14.93)
From the perspective of the earth and the northern hemisphere, the sun is traveling from east to west along the horizon, at different solar noon altitude depending on location and season. An optimal azimuth angle for a specific location would be the direction of the sun at solar noon, which is true south for the northern hemisphere. Looking away from possible diffuse solar radiation, the irradiation will be at its strongest at solar noon thanks to the fact that air mass will be the least at the time. See equation [am]. The intensity of the irradiation on the module will decrease rapidly before and after one hour from solar noon because of air mass, and the sun's angle of 15$°$ traveled per hour . Solar noon can be calculated based on Astronomy, but it is beyond the scope of this project. This can instead be found at various online resources. For example at www.timeanddate.com . Data covering Stavanger in December 21th 2019, states that solar noon is occoring at 12:34, at 180$°$ South, with an altitude angle of 8$°$ .
A battery is an electrochemical device that could be extensively described to fully understand. Instead this section summarizes the main parameters, characteristics and efficiency on an electrical level.
There are two main categories of batteries: Primary and secondary type, where the primary group covers the non-rechargable. Since recharging is one of the key reasons of a battery bank in an off grid PV system, the following information covers exclusively secondary type batteries.
Voltage: Battery nominal voltage, resulting from a series connection of cells with a nominal voltage.
Capacity: Battery nominal capacity, usually stated in [Ah], but can also be denoted in coulomb, [C].
State of charge, SOC: Gives a value in percent that tells how big part of the energy remains in the battery. Calculated as follows: $$SOC = \Bigg(\frac{[J_{available}]}{[C_{batt}] \cdot [V]}\Bigg) \cdot 100\%$$ where, [Javailable] is the energy available, [Cbatt] is the battery capacity in coulombs and [V] is the battery voltage.
Depth of discharge, DOD: Gives a value in percent that tells how big part of the batteries energy that has been used. Calculated as follows: $$DOD = \Bigg(\frac{[J_{discharged}]}{[C_{batt}] \cdot [V]}\Bigg) \cdot 100\%$$ where, [Jdischarged] is the discharged energy. SOC and DOD complement each other such that SOC + DOD = 100%
Cycle life: The number of charge/discharge cycles a battery can handle until the capacity goes under 80% of the nominal capacity. Often stated as different numbers depending on DOD.
Volumetric Energy Density: Used to compare batteries energy stored per unit volume. Critical specification for compact mobile devices. Denoted in [Wh [l−1].
Gravimetric energy density: Used to compare battery capacity per unit weight. Denoted in [Wh(kg)−1].
Battery efficiency: The efficiency of electrical energy storage, which gives information about losses during charge and discharge cycles (Sometimes called round trip efficiency). Calculated as shown below . $$\eta_{batt} = \Bigg(\frac{[J_{out}]}{[J_{in}]}\Bigg) * 100\% \label{batt_efficiency}$$
To summarize, here is four of the most common secondary type batteries:
Lead acid:
A well proven battery design, affordable and easily available for a big range of service areas.
Normally requires maintenance, vented surroundings and space consuming compared to other newer battery technology. As a result of poor maintenance and or overcurrents, comes "gassing", which means the battery will vapor an explosive gas. Other premature aging comes from electrode corrosion and sulphation. Sensitive to deep DOD compared to Li-ion. .
The lead acid battery's cell consists of two electrodes, anode and an cathode which is made of lead(Pb). The electrodes is positioned in a canister with electrolyte. The electrolyte, in liquid or gel form contains ions and can be decomposed by electrolysis.
Lead acid batteries come in different designs such as Absorbent glass mat (AGM) which is an high technology developement that is sealed, maintenance free and can handle extreme vibrations. There is also gel designs where the electrolyte is no longes liquid and therefore can be mounted in any position .
Lithium ion, Li-ion:
Rapidly developed in recent years, and extensively used in everything from cellphones to electric cars.
Benefits from high energy density compared to most other commercially available technologies. More robust to deeper DOD.
Maintenance free technology with one of the highest energy densities available in todays battery market.
Li-ion batteries comes in a number of different designs that utilizes different electrode materials. Examples of commonly used electrode materials is lithium iron phosphate, lithium manganese oxide, lithium cobalt oxide and graphite.
Lithium ions move between anode and catode during charge/discharge, and the high voltage and charge storage per unit mass is in part possible beacuse of the relatively small lithium ions.
Nickel metal hydride, Ni-MH:
Good energy density, comparable to the lithium ion.
The drawback with the nickel metal hydrite is that it suffers from a high rate of self discharge rate.
Nickel cadmium, Ni-Cd:
Considerably lower energy density than lithium ion.
Suffers from the "memory effect", meaning it needs to be fully discharged at every cycle to keep its capacity and lifetime.
Generally the battery capacity becomes smaller at lower temperatures, but the battery lifetime improves from operating under colder conditions. Overheating damages the battery, and this usually comes from overcharging. For analysis of a batterys characteristics, ambient temperature statistics for specific geographical location will be useful. This can be found online at publicly available sources. For Norway, Norsk Klimaservicesenter, is a valuable resource of weather and climate data. As an example, yearly average temperature data for Stavanger and December can be located. Data from the years 2015 to 2019 is localized and used to find an average based on these five years .
$$\label{averagetemp} \frac{(6.2 + 6.1 + 3.5 + 4.1 + 5.3)}{5} = 5.04 \hspace{1mm} [° C]$$
A solar charge controller is a power electronics device specifically built to handle the needs and conditions that a PV system requires. The charge controller interconnects the PV array, battery bank and the load, and to handle this it has several built in functionalities. A PV system is constantly changing from external parameters such as irradiance and ambient temperatrue. And energy usage will not happen synchrously with charging. It is therefor important to control a number of parameters. Below is an overview of some of the most important and commonly built in functionalities .
Maximum power point tracking, MPPT, which makes sure that most possible power is being extracted from the PV array, dynamically at all times . Further described under section 2.2.2.
Pulse width modulation, PWM, is used in early type charge controllers to control battery charging voltage. This technology does not optimize the PV power output such as the MPPT does, and is therefor not desired when chasing efficiency .
Voltage and current regulation, set to meet the specific battery requirements and limitations .
Temperature feedback from batteries. Automatically adjusts charge/discharge parameters depending on operating temperature, from choosen battery type .
An inverter is needed to convert the battery DC voltage to AC, 230 or 110 volts depending on geographical location standards. For bigger installations it is possible to get inverters for three phase output. Some manufacturers offer a charge controller with integrated inverter. Two important specifications to consider below
Continuous watts, which means the power that will be used normally.
Maximum instantaneous(surge) watts, required by the loads for a short instance of time. Could for example be caused by an electric motor starting up.
To be able to determine losses in cabling it is necessary to know voltage, current and resistace for the wires in question . The DC cable power efficiency ηwire can be calculated as follows: $$\eta_{wire} = 100\% \cdot \frac{P_{out}}{P_{in}} = 100\% \cdot \frac{(V_{in} - V_{drop} ) \cdot I}{V_{in} \cdot I}$$ where, Vdrop = I ⋅ Rwire Rwire can be found using the wire resistance formula below: $$\label{cableresistance} R_{wire} = \frac{\rho \cdot l}{A}$$ where,
ρ is resistivity in ohm-meters $[Ω m ]$. See table in figure [wireresistivity] for resistivity in commomly used wire materials.
l is the wire lenght in meters.
A is the cross-sectional area of the wire in square meters.
| Table of wire resistivity (ρ) | |
|---|---|
| Conductor material | $[Ω m ]$ at 300 Kelvin |
| Copper | 1.72 ⋅ 10−8 |
| Aluminium | 2.73 ⋅ 10−8 |
| Carbon | 3.5 ⋅ 10−5 |
| Gold | 2.27 ⋅ 10−8 |
| Silver | 1.63 ⋅ 10−8 |
According to the European Union, certain products require energy labels along with standard product information. The labelling standard at the time of writing is following the European Parliament directive 2010/30/EU. This energy labelling has a ranking scale from A to G with three additional grades added on top of Class A. These additional grades is A+, A++ and A+ + +. Stated in the Selina Consumer Guide , published by the European Commision, the average household standby electricty losses is found to be 11% during a survey made across EU countries. In the same study by the European Commision it is declared that the International Energy Agency expect that by 2030, 15% of total appliance electricity consumption in Europe could be due to standby functions . Listed below is common household energy consumers.
Washing mashine: Miele WDD020WCS is a highly efficient appliance with energy Class A+++. It uses 0.9 [kWh] at a standard 60[$°$C] program, at full load . → 0.9 [kWh] / 1 hour ≈ 900 [W] continuous (at 1 hour 60[$°$C] program).
Fridge/freezer: Bosch KGE36VW4A combination fridge/freezer, is a highly efficient appliance with energy Class A+++. It uses 161 kWh/annum. . → 161 [kWh] / 365 days ⋅ 24 hours ≈ 18.4 [W] continuous.
Water heater: Nibe Nibette 15, is a small 13.5 liter water heater that uses 1000 [W] on one phase. It is sufficient for quick showers and other washing needs. It uses 1.2 hours to heat water from 10[$°$C] to 80[$°$C], and has energy Class C .
Water boiler: Power consumption varies from model to model and 1500 [W] is a common figure.
Induction cooktop: Power consumption varies from model to model and 2000 [W] is a common figure.
Wireless router: Can be found with 5 watt consumption.
Lighting: 5 watt LED's is common replacements for 40 watt incandescent lamps that emits approximately the same lumen.
Laptop charger: Apple Macbook chargers is available in different watts. One option is listed at 45 W.
A web based application using traditional HTML in combination with Python as back-end programming language is a popular method and good alternative to PHP. The HTML to Python interface can be done using the Flask microframework. The Flask framework requires minimal code and installations to get up and running, and can thereafter be expanded with numerous modules depending on end product needs. It is therefore suitable for basic websites, as well as highly sofisticated applications. Flask is providing quickstart code snippets, along with good documentation . For developement of responsive design and front-end graphics, it is common to use both CSS and Javascript. This can be made easy by using the open source toolkit from Bootstrap . The Bootstrap framework can be used without installations through their CDN. There is many different ways of deplyoing a Flask application to make it accessible on the internet. Linux servers is commonly used, and can be set up using a cloud Linux server at one of many available hosts. Web applications of this kind, is usually deployed to a virtual machine on the server, where the user can install and configure using SSH.
This chapter is based on an off-grid PV system case study, which consists of a fictionalized small house with relatively small energy demands located in Stavanger, Norway. The case study system design, is based around specific minimum energy demands, where required PV array size and angles is calculated. Six main steps lead forward to final simulations of the complete system. As the case study covers a year round living scenario in Stavanger, it is known that the solar energy bottleneck will be during wintertime. Therefore from section 3.3 onwards, the month with the least available irradiation (December) has been used as a basis for design, simulation and analysis. In other situations where the PV array size is a bottleneck, a slightly different method is required (Explanied in section 3.4.4). In parallel with the case study project, a simple web application is developed as an online tool. The web application is built for personal use during this project, but also as a future resource for anyone interested. The application has functionalities to facilitate steps 1 to 4 below.
| 1. Mapping of system loads. . Battery-bank dimensioning. . Solar irradiation evaluation. | 4. PV array sizing and considerations. . MPPT Charge-controller & inverter. . System simulation. |
The system block diagram in figure [blockdiagram], is made to get a simple overview of the PV system main components. Indicated in this diagram, is the different efficiency parameters(η) that has been considered in the coming sections. = [draw, fill=blue!20, rectangle, minimum height=8em, minimum width=13em] = [pin edge=to-,thin,black]
| Summary of considered efficiency parameters | |
|---|---|
| Efficiency: | Parameter: |
| PV module maximum power point | ηmpp |
| PV module operating temperature | ηpv − temp |
| PV module optimal angle | ηangle |
| PV array to controller cable | ηarray − cbl |
| Inverter | ηinv |
| Charge controller | ηcharge − ctrl |
| Battery cable | ηbatt − cbl |
| Battery roundtrip | ηround − trip = ηbatt − chng * ηbatt − dchng |
| Battery temperature effect on capacity | ηbatt − temp |
| Inverter to load cable | ηload − cbl |
| Standby power losses | ηstandby |
An important task when designing a PV powered system for off-grid use, is to gather and list information about energy comsumption. The list should contain all appliances including small electronic gadgets. This will give a good overview of where the biggest amount of power goes. In many cases the energy usage can be minimized by using more energy efficient appliances and hence a suitable pv/battery system can be designed. For example, it might be feasable to upgrade to a newer and more energy efficient fridge. This case study, based on a fictionalized house, is equipped for simple but year-round living. It is not electricity-dependent for heating. The heating is instead envisioned to be handled by, for example, a woodstove. Page #1 in the web application (Appendix A) can be useful to find daily watthours similar to what is done in figure [consumers].
| Consumer | Watt | Hours | [Wh] |
|---|---|---|---|
| LED lighting | 4pcs. ⋅ 5 = 20 | 12 | 240 |
| Wireless router | 5 | 24 | 120 |
| Laptop charger | 45 | 5 | 225 |
| Washing machine | 900 | 1 | 900 |
| Water boiler | 1500 | 0.3 | 450 |
| Induction cooktop | 2000 | 2 | 4000 |
| Water heater | 1000 | 3 | 3000 |
| Fridge/freezer | 18.4 | 24 | 441.6 |
| Total [Wh]: 9376.6 | |||
The electrical power in an off-grid PV system will essentially have a DC side and a AC side. The DC power transfer will happen mostly between PV array to controller/inverter. And AC power will be from inverter out to appliances. The power losses in the AC side of the electrical system, will be similar to the losses of any conventional household. This is mostly from standby losses, as covered in section 2.5. Assuming that 11 percent of total energy consumption is caused by cabling and standby losses in the 230 volt, AC part of the system, the total watthours is recalculated as follows:
$$\frac{9376.6}{100\% - 11\%} = \frac{9376.6}{89\%} \approx 10536 \textnormal{ [Wh]} = 10.536 \textnormal{ [kWh]} \label{24henergy}$$
With the standby and AC-cabling losses now included in the daily total energy usage, it is covered for ηstandby and ηload − cbl, shown in the block diagram (figure [blockdiagram]). The proposed 24 hour timeline in figure 3.1 is set up based on the table in figure [consumers] and a possible scenario of use.
For the purpose of simulations later in this report, the consumption timeline in figure 3.1, is translated into a kW consumption curve. The resulting power curve shown in figure 3.2, is produced using values from the table in figure [consumers] and the timeline in figure 3.1.
With a focus on correct daily energy consumption (10.536 kWh), this curve is actualized using Python, through an interpolated list of values. The curve is then numerically integrated, using the trapezoidal method (section 2.1), to verify the daily kilowatthours towards the result in equation [24henergy].
The battery-bank in an off-grid PV system is built up of a number of batteries, configured in series and or parallel to supply the appropriate voltage needed. The purpose of the battery-bank is to be able to store and later distribute the needed energy. Energy storage is needed since the solar irradiance curve versus load curve, will not match up. It also helps cover up for seasonal fluctuations as for example, diffuse solar radiation in combination with higher load demands. Because the case study location is Stavanger where the weather is challenging for PV power, the battery-bank has been calculated based on a two day backup scenario. Two days of heavy clouds is not unusual, especially during wintertime. With the unwanted "memory effect" in Ni-CD technology and high rate of self-discharge in Ni-MH, it is clear that Lead Acid and Li-ion batteries make better choices for a PV system (Section 2.3). As the Ragone plot in figure 2.11 illustrates, the lead acid battery will be considerably bigger and heavier than any Li-ion battery with the same capacity. And as this project has been focused on efficient technology rather than affordable components, lithium-ion has been used for the case study. Specifically the Victron Energy, 25,6v/200Ah Lithium-Iron-Phosphate Battery Smart. Considering power transfer losses, it is in most cases beneficial to work with higher voltages since it results in lower currents. Based on equation [vdrop] in chapter 2, less current results in less Vdrop, which in turn results in better DC cable efficiency. and 48 volt is commonly used in larger systems, and for the sake of best possible efficiency, a 48 volt battery bank is decided for the case study. Knowing that battery capacity will decrease when operating at colder temperatures (section 2.3), ambient temperature has been used for battery bank sizing.
Battery round trip efficiency (ηround − trip) is stated at 92 percent, for all LiFePO4 batteries from Victron. For the purpose of simulation later in the report, battery round-trip efficiency is split up as follows: ηround − trip = ηbatt − chng ⋅ ηbatt − dchng For simplicity the charging/discharging efficiencies is assumed similar and therefor the round trip efficiency is split equally in two. ηbatt − chng = ηbatt − dchng = 96[%] Resulting in: 96[%] ⋅ 96[%] ≈ 92[%] = ηround − trip
Best stated cycle-life is achived by operating at 50 percent DOD.
Ambient temperature effect on capacity (ηbatt − temp):
Victron datasheet states Nominal capacity at 25[$°$C] to be 200 [Ah], and 160 [Ah] at 0[$°$C].
Assuming the rate of capacity change is proportional to change in temperature, one can find a ratio as follows: = 1,6 [Ah/$° C]$ The remaining percentage of the nominal 200 amphour capacity, at the operating temperature, can then be found using the ratio above. Average ambient temperature for December in Stavanger is 5.04 [$°$C](equation [averagetemp]). (25$°$ C - 5.04$°$ C) = 19.96 [$°$C] drop from nominal 25 [$°$C] at 200 [$°$C]. $°$ C ⋅ 1.6 = 31.936 [Ah] drop from nominal 200 [Ah]. $$\rightarrow \eta_{batt-temp} = \frac{200-31.936}{200} \cdot 100[\%] \approx 84[\%], \textnormal{ of nominal 200[Ah] capacity.}$$
To find the necessary battery-bank capacity, the below steps is followed. Page #2 in the web application (Appendix A) can be used to find and experiment with these five steps.
Daily energy usage from equation [24henergy] compensated for the battery round-trip efficency: 10.536 [kWh] ⋅ ≈ 11.451 [kWh]
The result from step 1, compensated for the preferred 50 percent DOD: 11.451 [kWh] ⋅ ≈ 22.902 [kWh] Note: DOD can be up to 80 percent using Li-ion, to help minimizing battery bank capacity.
The result from step 2, compensated for capacity drop at lower operating temperature: 22.902 [kWh] ⋅ ≈ 27.264 [kWh]
The result from step 3, multiplied by the desired number of backup days. In this case 2 days: 27.264 [kWh] ⋅ 2 ≈ 54.529 [kWh]
Divide the result from step 4 with the desired battery bank voltage. In this case 48 volt is desried: 54.529 [kWh] / 48 ≈ 1136 [Ah]
Note: Inverter and charge-controller losses has not been considered at this stage, but included later in the simulations section. With the calculated battery-bank capacity figure, battery configuration comes next. A series connection of two 24[V]/200[Ah] batteries results in 48[V]/200[Ah]. And by paralleling 5 of these battery pairs, a battery-bank of nominal 48 volt and 1000 amphours is obtained. This is slightly below the calculated needed battery capacity, but adequacy is later analyzed through simulation.
To find the loss in the cable connecting the battery bank to inverter/charge-controller (ηbatt − cbl), the maximal instantaneous current drawn by the load is used. Battery cable length of 3 meter has been used for the example case study. Based on the power curve in figure 3.2, a daily power peak of 2043.4 watts is drawn when the induction cooktop is used. This causes a current at: [W] / 48 [V] ≈ 42.57 [A], daily peak current. To calculate the battery cable loss, it is necessary to know the cable cross-sectional area. Which will depend on the specific cable manufacturers specifications and recommendation. In this case, a recommendation table from Victron, and the peak current of 42.57 amps, is used decide on 16 squaremillimeter area. The recommendation states, this should be sufficient with some margin . Making use of equation [cableresistance] and the resistivity ρ, for copper from figure [wireresistivity], the battery cable efficiency percentage is found through the steps below: $$R_{wire} = \frac{1.72 \cdot 10^{-8} \cdot 3}{16 \cdot 10^{-6}} \approx 3.2 \hspace{1mm} [mΩ]$$ $$V_{drop} = I \cdot R_{wire} = 42.57 \hspace{1mm} [A] \cdot 3.2 \hspace{1mm} [mΩ] \approx 136 \hspace{1mm} [mV]$$ $$\label{batterycableefficiency} \eta_{batt-cbl} = 100\% \cdot \frac{48 - 0,136 \cdot 10^{-3}}{48} \approx 99.9997 [\%]$$ With the result in equation [batterycableefficiency] it is tempting to say that the battery cable losses is negligible, but it is accounted for later in the report during simulation, and where the total system efficiency is summarized. Note: Calculating cable loss using the peak-current is a close approximation. To find the exact loss, an integration based on the instantaneous current would be required.
The solar irradiation data used for the Stavanger case study is of SIS specifications aquired from CMSAF. SIS data properties has been explained in section 2.2.1, and most importanly to understand, that this data is given in watts per squaremeter, reaching the earth surface on an horizontal surface, including the photon wavelengths usable by PV technology. This means, the angles of the module will say quite alot about the amounts of irradation that is actually possible to absorb and use, especially at latitudes far from the equator. The PV module angles is accounted for in the next section. A histogram of monthly average irradiation for Stavanger is produced from the CMSAF supplied NetCDF data files, using Python with additional packages(see Appendix B). This histogram, in figure 3.4, is based on ten years of statistics covering monthly average irradiation.
At Page #3 in the web application (Appendix A), monthly average irradiation can be found and compared. With the current version of the application, two locations can be compared and evaluated at a time, with data covering 30 different locations available.
With a starting point from this data, the month with the least average irradiation is used further. This is found to be December with an average of 7.8 watts per squaremeter. To be able to later simulate an 24 hour scenario of the PV system, a irradiation charging curve is needed. To achieve this, the irradiation data together with sunhour information, is translated into an 24 hour continous curve. In addition to the solar noon time (12:34), found in section 2.2.4, the below information is extracted online, for Stavanger in December 21th 2019 .
Sunrise at 09:29, at 138$°$ SE
Sunset at 15:40, at 222$°$ SW
Daylight length of 6 hours, and 11 minutes.
The 24 hour irradiation curve in figure 3.5 is produced using the same method as the consumption curve (figure 3.2), based on the three points below. The average value of this curve is calculated to verify 7.8 as desired. This has served as a basis for coming calculations and finally simulations to test out PV array and battery-bank size.
Satellite aquired average irradiation data from ten years of statistics, delivered by CMSAF. See Appendix B.
Sunrise, sunset and solar noon hours as described on this page.
Typical sunhours pattern where the suns radiation stays approximately the same one hour before and after solar noon. See section 2.2.4.
For the purpose of the case study, the sections below cover the gain from optimal angles, required PV array size, and PV array output. A fixed PV array installation has been chosen for this study, based on arguments discussed in Chapter 5. Aside from the case study, for situations where the PV array size is the bottleneck, an alternative method is described in section 3.4.4.
Ideally it is desired for the incident angle θi to be 0, which means an optimal angle is obtained.
In reality with a fixed PV module position it is all about minimizing θi through out the day. Latitude for Stavanger is 59$°$, and an optimal elevation angle(θ) for December is desired. Following section 2.2.3, the result is: $$\label{optimal_angle} 59° + 14.6° = 73.6° = \theta$$ The next step is to find out what this specific optimal elevation angle can give in return, based on the horizontal surface SIS data. The different angles in relation to horizontal from figure 3.6, is being used below to derive equations, and finally to end up with the two cases in equation [case1] and [case2].
$$\theta_{i} = 90° - (\theta_{Z}+(90° - \theta))$$ $$\rightarrow \theta_{i} = 90° - \theta_{Z}-(90° - \theta)$$ $$\rightarrow \theta_{i} = 90° - \theta_{Z}-90° + \theta$$ → θi = θ − θZ Direct beam solar radiation (IB) as explained in section 2.2.1, is the radiation that will reach earth without diffusion. In this case IB will be replaced by an expression of the SIS irradiation (ISIS). Based on some basic trigonometry and figure 3.6, it is possible to set up the relations in equation [I_pv] & [I_b]. IPV = IB ⋅ cos(θi) $$\label{I_b} I_{B} = \frac{I_{SIS}}{cos(\theta_{Z})}$$ Where IPV is the irradiance in watts per square-meter on to the PV module surface. Substituting to get an expression involving the two angles: $$\label{optimal_angles} I_{PV} = \frac{I_{SIS}}{cos(\theta_{Z})} \cdot cos(\theta_{i}) = \frac{cos(\theta_{i})}{cos(\theta_{Z})} \cdot I_{SIS}$$ From the last expression in equation [optimal_angles], two cases has been considered. Case 1: When the sun beams is parallel to the normal vector of the PV module. Meaning the exact optimal angle, and θi = 0$°$. Which also means that θZ = θ and the equation [case1] can be written. This case would be valid for a well working two-axis tracker. $$\label{case1} I_{PV} = \frac{1}{cos(\theta)} \cdot I_{SIS}$$ Case 2: Second case is when θZ ≠ θi and θi> 0. For installations without solar tracking. $$\label{case2} I_{PV} = \frac{cos(\theta_{i})}{cos(\theta)} \cdot I_{SIS}$$
For further evaluations, Case 2 has been used, which is most realistic for a fixed PV module installation. Now, combining the facts that the sun is traveling 15 degrees per hour, and that full irradiation is present for only one hour before/after solar noon (section 2.2.3). During these ±15 degrees travel of the sun in relation to solar noon, the solar altitude angle will change just slightly. Based on this, the approximation of θi = 5$°$ has been used as an average in the Case 2 equation ([case2]). Using θi = 5$°$ in the calculation will add a small irradiation loss which is natural, since a fixed position will never fulfill θi = 0$°$.
Azimuth angle for a fixed installation will be optimized by pointing the module at true south, which is equivalent to the sun's direction at solar noon. As explained in section 2.2.3 with background from the book Photovoltaics Systems Engineering, less than 2 percent irradiation loss is common at up to 22.5$°$ degrees azimuth angle offset. With the short duration of sun-hours in Stavanger during December month, azimuth angle offset will not likely be bigger than 22.5$°$. This can also be seen from the "narrow" sun curve illustrated in figure 3.5. Based on this information, an approximation is made to use a 2% loss (ηazimuth = 98[%]) for the fixed azimuth angle.
Utilizing equation [case2] from case two, the angles found, and the azimuth loss, the optimal angle efficiency (ηangle) is found: $$\label{n_angle} \eta_{angle} = \eta_{azimuth} \cdot \frac{cos(\theta_{i})}{cos(\theta)} = 98[\%] \cdot \frac{cos(5°)}{cos(76.4°)} \approx 415.18 [\%]$$ To summarize ηangle : This is the factor that, thanks to the optimized angles, will improve and increase the amount of absorbed photon energy at latitudes and seasons where the sun is not perpendicular to the earth horizontal surface, when using SIS data. This effect of incident angle is illustrated in figure 2.10. Note: The value found in equation [n_angle] is specific for this case study, but the method can be used to find gain or loss at any location and PV module elevation. ηangle, is next used to approximate the actual average irradiation (IPV), on to the PV module surface. $$\label{ipv} I_{PV} = \eta_{angle} \cdot I_{SIS} = 423.66 \% \cdot 7,8 \textnormal{ [W}m^{-2}] \approx 32.38 \textnormal{ [W}m^{-2}]$$
At this point, an estimation of the needed PV array surface area is calculated based on IPV and the PV module characteristics. Equation [arrayA] is formulated to output an approximation of needed PV array area in square meters, required to recharge the consumed energy during one average day. $$\label{arrayA} A = \frac{E_{D} }{T \cdot I_{PV} \cdot \eta_{mpp} \cdot \eta_{pv-temp}}$$
A = The PV array area in [m2]
ED = 10536 [Wh], Daily minimum energy usage (equation [24henergy]).
T = 24 hours, [h].
IPV = 32.38 [Wm−2], Irradiation on the PV modules (equation [ipv]).
ηmpp = 19.8 [%], Maximum power point conversion efficiency, of the LG Neon 340 watt PV module used in this case study.
ηpv − temp, defined and found below, based on the "Temperature coefficient of power" covered in section 2.2.3. $\eta_{pv-temp} =\alpha_{p} \cdot \Delta = (-0.36\cdot(5.04°-25°)) \approx 7.19$ [%],
Temperature coefficient($\alpha_{p} = -0.36\%/°$), and nominal temperature(25$° C$), from PV module datasheet .
Ambient temperature average(5.04$° C$) for Decemeber in Stavanger (equation [averagetemp]).
Resulting in: $$\label{neededarea} A = \frac{10536}{24 \cdot 32.38 \cdot 19.8\% \cdot 107.19\%} \approx 63.88 \textnormal{ } [m^{2}]$$ Note: square meters of effective PV module surface area, at 76.4 degrees angle, will cause practical problems in many real situations. Even though this area can be split up between several sub-arrays. For situations where PV array space is strictly limited, see section 3.4.4. One LG Neon PV module has effective surface dimensions of approximately 1000 x 1650 mm, which means approximately 1.65 m2 . Based on the result from equation [neededarea], next is to find an estimate of how many PV modules that is needed. $$63.88 [m^{2}] / 1.65 [m^{2}] \approx \textnormal{39 PV modules needed.}$$ $$\rightarrow 39 \textnormal{ modules} \cdot 1.65 \textnormal{ }[m^{2}] \approx 64.4 \textnormal{ }[m^{2}]$$ Meaning, 39 modules will give an area slightly over what is found in equation [neededarea]. Page #4 in the web application (Appendix A), consists of a slightly simplified PV Array Sizing Calculator. The application is utilizing an algorithm, assuming that incident sun angle θi relative to the PV module has an average value of 5 degrees, as well as neglecting losses from a fixed azimuth angle and high operating temperatures. The user is required to input the location latitude, irradiation, energy usage, and PV module efficiency. An optimal angle is internally calculated, and the estimated array area is returned.
python @app.route(’/4’, methods=[’POST’]) def page4_calc(): latitude = float(request.form[’latitude’]) i_sis = float(request.form[’i_sis’]) e_d = float(request.form[’e_d’]) mpp_e = float(request.form[’mpp_e’]) if latitude >= 0: theta = latitude + 14.6 elif latitude < 0: theta = latitude - 14.6 array_area = (e_d * math.cos(theta)) / (24 * math.cos(5) * i_sis * (mpp_e/100)) array_area = round(array_area,2); return render_template(’page4.html’, array_area = array_area)
Based on values found in section 3.4.2 and 3.4.1, an PV array average power output (Paverage) has been found. Paverage = A ⋅ IPV ⋅ ηmpp ⋅ ηpv − temp → 64.4[m2] ⋅ 32.38[Wm−2] ⋅ 19.8[%] ⋅ 107.19[%] ≈ 0.443[kW] The PV array output power curve in figure 3.7, is produced for later use during simulation. The curve is a rescaled version, based on the horizontal surface irradiation curve in figure 3.5, which now holds the Paverage value.
Whilst the dark green curve line is showing the charging value at different hours, the green shaded area underneath the curve would be kilowatthours in a day, if integrated. The plot also illustrates an average daily maximum charging, of close to 2.1 kilowatts, which is maintaned for about 2 hours during mid day. This curve represents a close approximation of an average day's available charging from the PV array in December. Note: For sizing of charge-controller and cables, summer peak power should be evaluated.
Irradiation and PV array output during a particular day in the month could turn out to be both better or worse than the average charging curve in figure 3.7. Therefore, in preperation for simulations, two alternative curves is produced, from now on called Good day and Bad day.
Figure 3.8: PV array output Good day charging curve, based on an average days charging and a factor of 1.5. → 0.443 [kW] ⋅ 1.5 = 0.6645 [kW] = Good day average.
Figure 3.9: PV array output Bad day charging curve, based on an average days charging and a factor of 0.5. → 0.443 [kW] ⋅ 0.5 = 0.2215 [kW] = Bad day average.
This alternative method sequence, has not been used for the case study, but can be used in cases where the physical PV array space is strictly limited to for example, a specific roof or wall square meters.
Based on equation [arrayA], the below formula is derived, and can be used to determine energy available, given specific square meters (A) available. ED = A ⋅ T ⋅ IPV ⋅ ηmpp ⋅ ηpv − temp Where, T, IPV, ηmpp, and ηpv − temp can be found as previously described in section 3.4.
With the energy available (ED), found in step one, Page #1 in the web application can be used to "test out" combinations of appliances and possible amounts of energy consumption.
Having found the energy consumption, in step two, battery bank capacity can be calculated as described in section 3.2.
With a background from battery characteristics described in section 2.4, a charge controller configured for the battery type will protect from overcharging and high temperatures, which will help increase the lifetime of the battery-bank significantly. Overcharging essentially means that voltage and or current during charging is not within specifications. This brings us to the fact that a charge controller is needed. In my opinion, this battery protecting technology, and the MPPT, is what makes the difference in high-end products. The Victron EasySolar-II , chosen for the case study, has integrated MultiPlus-II inverter/charger, as well as SmartSolar MPPT -Tr solar charge controller. This all-in-one solar power control unit is found suitable by evaluation continous current and maximum surge current limits . The inverter, and charge controller electronics is consuming some power, and will therefor cause small power losses.
Inverter efficiency (ηinv) is stated in the product datasheet to 95[%].
Charge controller efficiency (ηcharge − ctrl) is stated to 98[%].
Finally in this section the PV-array to charge-controller cable efficiency (ηarray − cbl) has been found. This cable is assumed to be 5 meter long, for the sake of this example. Furtherly a recommendation of 35 squaremeter cable is followed , for the Victron charge controller that will be used as example. 48 volt design from array to MPPT is also choosen based on efficiency considerations and Victron datasheet . To find the PV array cable efficiency, it is necessary to find the array cable resistance. Following equation [cableresistance] and resistivity for copper cable from figure [wireresistivity], the below is found: Copper cable: ρ = 1.72 ⋅ 10−8 $$R_{wire} = \frac{1.72\cdot10^{-8} \cdot 5}{35\cdot10^{-6}} \approx 0.0025 [Ω]$$ The maximum average charging current, and voltage drop, is found using maximum PV array power output (Found in figure 3.7). Imax = Pmax/voltage ≈ 2.1[kW]/48[V] = 43.75[A] $$V_{drop} = I_{max} \cdot R_{wire} = 43.75 [A] \cdot 0.0025[Ω] \approx 0.11 [V]$$
$$\rightarrow \eta_{array-cbl} = 100[\%] \cdot \frac{48 - 0.11}{48} = 100[\%] \cdot \frac{47.89}{48} \approx 99.77[\%]$$
In preparation for the system simulations, all efficiency parameters is divided into two main categories as follows.
Category 1: Parameters during battery charging from solar irradiation: ηmpp, ηpv − temp, ηangle, ηarray − cbl, ηcharge − ctrl, ηbattery − cbl, ηbatt − chng, ηbatt − temp
Category 2: Parameters during battery discharging to loads: ηbatt − dchng, ηbattery − cbl, ηinv, load − cbl, ηstanby, ηbatt − temp
The idea of the system simulation is to test and verify the dimensioning that has been done up to this point. With the simulation set up and working, this also gives a chance to experiment with the battery-bank capacity. The simulation is done using Python, with some additional packages such as Matplotlib to visualize the plots. The desired outcome of the simulation is to visualize the following two subplots over a 24 and 72 hour scenario.
Subplot 1:
Content: Charging/discharging of the battery-bank in kilowatts.
Approach : The list in Python representing charging values for figure 3.4, is multiplied by the Category 1 power transfer loss factors. In the same way the Category 2 factors is multiplied by the discharging list values for the curve (fig. 3.2) in section 3.1. The new charging list is then subtracted by the "new" discharge list, to produce the desired battery charging/discharging subplot for the simulation.
Subplot 2:
Content: SOC of the battery-bank in percent.
Approach: The Subplot 1 values in KW is numerically integrated (using the Trapezoidal method), to obtain capacity usage in kWh. Based on chosen battery bank capacity, the incident battery state could then be calculated. From the chosen battery-bank capacity and capacity usage, the SOC is found for Subplot 2.
In this chapter, a summary and visualization of system losses is utilized for analysis. The simulation methodology explained in section 3.6, is applied to visualize and analyze different scenarios of sun conditions. Finally, in section 4.3, the potential untapped solar energy during summer has been evaluated.
To visualize and analyze the case study PV system losses, three Sankey diagrams is produced based on the Category 1 and Category 2 losses, as defined in section 3.6, as well as one final overall system loss diagram. Note, that these diagrams of losses is based on December month conditions, and percentages will therefore deviate slightly during other times of the year.
Category 1 loss table, diagram and comments.
Category 2 loss table, diagram and comments.
Overall PV system loss table, diagram and comments.
| Category 1 losses sequence | ||||
|---|---|---|---|---|
| Efficiency | Parameter | Value [%] | Remaining [%] | Loss [%] |
| Maximum power point | ηmpp | 19.8 | 19.8 | 80.2 |
| Array cable | ηarray − cbl | 99.95 | 19.79 | 0.01 |
| Charge controller | ηcharge − ctrl | 98 | 19.39 | 0.4 |
| Battery cable | ηbatt − cbl | 99.9997 | 19.38998 | 0.00002 |
| Battery charging | ηbatt − chng | 96 | 18.61 | 0.78 |
| Total loss: 81.39% | ||||
Note: Maximum power point efficiency usually is not considered a system loss, but chosen to be included in this partial loss consideration.
Category 1 losses analysis comments:
The most significant potential for improvement is at the maximum power point efficiency. This PV module component parameter makes it evident that the development of PV technology is a relevant field that will have a big impact on solar energy conversion in the future.
The second-largest loss happens at the battery bank during charging. This is due to battery type characteristics and shows us that battery choice is essential when designing a system with a focus on efficiency.
| Category 2 losses sequence | ||||
|---|---|---|---|---|
| Efficiency: | Parameter | Value [%] | Remaining [%] | Loss [%] |
| Battery discharging | ηbatt − dchng | 96 | 96 | 4 |
| Battery cable | ηbatt − cbl | 99.9997 | 95.9999 | 0.0001 |
| Inverter | ηinv | 95 | 91.2 | 4.8 |
| Load cable | ||||
| & standby power | ||||
| & ηstandby | 89 | 81.17 | 10.03 | |
| Total loss: 18.83% | ||||
Category 2 losses analysis comments:
A relatively big loss is caused by cabling and standby-losses at the loads. Shows the importance of choosing energy efficient appliances and to disconnect gadgets not in use to minimize standby power consumption.
Inverter efficiency causes the second-largest loss during power consumption from the battery-bank. Indicates the importance of considering inverter characteristics when choosing a component.
Overall system losses can be summarized and viewed in slightly different ways, since charging and discharging happens simultaneously and changes dynamically as sun and consumption changes over time. It is, in this case, made simple by assuming that battery discharging happens after charging.
| Overall system losses sequence | ||||
|---|---|---|---|---|
| Efficiency | Parameter | Value [%] | Remaining [%] | Loss [%] |
| Array cable | ηarray − cbl | 99.95 | 99.95 | 0.05 |
| Charge controller | ηcharge − ctrl | 98 | 97.95 | 2 |
| Battery cable | ηbatt − cbl | 99,9997 | 97.9499 | 0.0001 |
| Battery charging | ηbatt − chng | 96 | 94.03 | 3.92 |
| Battery discharging | ηbatt − dchng | 96 | 90.27 | 3.76 |
| Battery cable | ηbatt − cbl | 99.9997 | 90.2699 | 0.0001 |
| Inverter | ηinv | 95 | 85.76 | 4.5 |
| Load cable | ||||
| & standby power | ||||
| & ηstandby | 89 | 76.33 | 9.43 | |
| Total loss: 23.67% | ||||
Overall PV system losses analysis comments:
Number one cause of power losses comes from standby losses, based on statistics as stated in the background theory chapter.
Second largest cause of system losses comes from system components such as inverter, battery and charge-controller.
Cabling causes relatively little loss.
The first simulation result (figure 4.4) following the steps outlined in section 3.6 confirms that the PV array sizing is sufficient for the battery-bank and energy usage for the case study at an average day. Initial SOC at midnight (start of simulation) is set to be 80 percent.
The simulation shows that after 24 hours of simultaneous charging and energy consumption, the battery SOC is back to 80 percent. This is a good sign, but important to note is that this is based on an average days irradiation, meaning all days of the month is looking the same, which in turn means that irradiation could be both better or worse. These better or worse scenarios are further analyzed through the following simulations.
The battery-bank is in chapter 3 sized to last as a two day backup with the average energy consumption. To verify this, the simulation in figure 4.5 over 72 hours of zero solar charging is done.
SOC had gone down to 50 percent after approximately 48 hours, which is calculated for with the desired DOD of 50 percent. Testing the SOC recovery time, another simulation (figure 4.6) is run over 72 hours with an initial SOC of 50 percent and the Good day sun conditions.
The simulation now indicates that it takes about three days of Good day sun conditions to recover from two days of zero charging from the sun.
Since it is more realistic to receive small amounts of charging rather than zero charging, even during a cloudy period, it is desired to simulate this scenario. The following simulation covering 72 hours using the Bad day sun conditions is run.
Evaluating figure 4.6 at 48 hours, the SOC had now decreased only about 20 percent. Indicating that the battery-bank capacity could possibly be smaller and still keep up as a two-day backup. The simulated battery capacity is decreased to 18 kilowatt-hours (figure 4.7), where it now shows a DOD of 50 percent after 48 hours.
The focus throughout the report is centered around system design, optimized for average winter (December) conditions, which can recharge the minimum daily consumption found in section 3.1. This design approach, at this geographic location, results in significantly more electrical energy available during summer, even though the PV array angle is optimized for winter. This untapped energy is in this section calculated through some approximations for analysis purposes.
Optimal PV module elevation angle for June (at latitude 59$°$) would be 44.4$°$ (section 2.2.4), and since the system is instead winter optimized with an elevation angle fixed at 76.3 degrees, there will be an angle offset of 31.9 degress from the June optimal. In addition, the daily sun curve (figure 4.8) is considerably wider than the corresponding December curve (figure 3.5). This means more loss caused by the fixed azimuth angle, and an approximation of 20 percent loss (80 percent efficiency) is used to calculate the June angle-efficiency (ηangle, June). Based on the same theory, and method as equation [n_angle]. $$\eta_{angle, June} = 80[\%] \cdot \frac{cos(5 + 31.9°)}{cos(76.4°)} \approx 2.72 [\%]$$ Resulting in merely a 2.72 percent average improved irradiation absorption through the 76.3 degrees elevated PV modules, compared to a horizontal mount, in June. (Down from ηangle = 415.18 percent in December.) This makes sense, since the solar altitude angle is significantle larger, during summer. Average June irradiation on to the PV modules, IPV, is calculated below. $$\label{I_pv_june} I_{PV} = 102.72 [\%] \cdot 217.3 \textnormal{ [W}m^{-2}] \approx 223.21 \textnormal{ [W}m^{-2}]$$ Based on equation [neededarea], the PV array June average daily output ED, is found. $$E_{D} = 64.4[m^{2}] \cdot 24[h] \cdot 223.21[Wm^{-2}] \cdot 19.8[\%] \cdot 107.19[\%] \approx 73 \textnormal{ } [kWh]$$ Subtracting the minimum daily consumption from equation [24henergy], to find the potential "untapped" energy. $$E_{untapped} = 73 \textnormal{ } [kWh] - 10.536 \textnormal{ } [kWh] \approx 62 \textnormal{ } [kWh]$$ This means that the energy consumption could potentially be increased by a factor of 5 during June average conditions. Since this case study covers off-grid system design, this energy could not be sold as grid-tied systems can. But, this available energy could with great advantage be used for something like additional water heating.
The web application version 1.5 is launched to http://www.techoffgrid.com and can be of use when utilizing this methodology, or individual calculations. I consider the application not fully developed, but a good foundation with great potential of being expanded with more functionalities.
A backup sized battery-bank is an essential consideration at locations with highly diffuse radiation, but not as crucial for a weekend-house/cabin since the weekdays would allow recharging. From an economic point of view, considering the simulation results in figure 4.6 & 4.7, it might be a good idea to configure the battery-bank into a slightly smaller capacity and then expand if needed.
The gain from a solar tracking device is small at locations of northern latitudes during seasons of highly diffuse radiation (as described in section 2.2.4.). A tracking device would also add moving parts to the system, that in turn adds possible sources of mechanical issues and required maintenance. Tracking devices could, on the other hand, be a good alternative for someone wanting to maximize possible PV module output at very limited space, or in large-scale applications where it is economically defendable.
Lower temperatures are beneficial for PV module efficiency but can negatively affect battery capacity. Therefore a good idea to store a battery-bank in a tempered area at cold climate locations. Aging of a battery can be highly affected by how it is used, what temperatures it operates in, and at what kind of currents it operates. Battery datasheets usually state cycle life at different DOD, at a given operating temperature range, as well as recommended charge/discharge currents. An ideal lifetime of a battery could, therefore, theoretically be determined from the stated cycle life if we had a fixed DOD and knew how often it would be cycled. In reality, the DOD and temperature will vary on different occasions. These parameters need to be considered when designing a battery bank to get the most out of it.
Publically available solar irradiation data can be of great help when sizing and running simulations. However, it is important to understand the difference between radiation specification types. It is also crucial to know how and at what time of year the system will be used. Unlike the case study, a summer use only scenario would require a significantly smaller PV-array, considering more sun-hours and higher irradiation, as shown in figure 3.4 histogram.
The 39 modules and 64.4 square meter PV array dimension suggested for the case study, would require quite a big roof. It could, for instance, be divided into two sub-arrays where one is roof-mounted, and the other part is ground-mounted.
Simulations show that off-grid year-round living at northern latitudes using solar energy for household electricity is possible if conscious decisions are made. An optimal angle is of crucial importance at northern latitudes for efficient photovoltaic energy conversion, mainly because of the significant difference in irradiation availability for summer versus winter.
There are many things regarding the simulation of different weather and shading scenarios that could be analyzed. Shading and PV cell mismatch are known to have significant adverse effects, and in this case study, it has been assumed absent. A function of temperature over time could be added to the simulation to see how PV and battery efficiency changes. It would be interesting to do similar simulations based on real charging and consumption data. This could, for instance, be done by logging charging from a PV module and ambient temperatures, over a period of time. Energy consumption data could be monitored and logged from a house of interest. The simulations performed in this thesis project is accomplished through some relatively simple code lines and standard packages for Python. This could be developed to include a GUI. Alternatively, more complex simulations, including more parameters, could be done using available open-source simulators for photovoltaics.
Application developed using HTML and Python back-end, combined using the Flask framework . Some Javascript and CSS through Bootstrap is used for front-end design and to obtain screen size responsive design .
Deployed to the acquired domain techoffgrid.com, hosted on a cloud Linux server by linode.com . Server using Nginx 1.16.1 and Ubuntu 19.10 as operating system. Running Python 2.7.17 with Flask 1.1.1 and Pygal 2.4.0.
The application consists of six pages that inherits from layout.html. Start and about page is informative only. Page 1 to 4 contain various PV system sizing resources. Example screenshots of the six web application pages included below. The application was initially based on starter code snippets from Flask and Bootstrap as described in section 2.6. It is then further developed to obtain the desired functionalities. A couple of different Flask imports is necessary for template inheritance and user request handling. Pygal bar charts is used for the interactive histograms on the application page #3 .
for tree=font=, grow'=0, folder indent=.9em, folder icons, edge=densely dotted [Main application folder [calculator1.py, is file] [static [dropdown.js, is file] [main.css, is file]] [templates [layout.html, is file] [start.html, is file] [page1.html, is file] [page2.html, is file] [page3.html, is file] [page4.html, is file] [about.html, is file]] ]
Irradiation data used in the report and web application is sourced from EUMETSAT's Satellite Application Facility on Climate Monitoring (CM SAF) . The histograms produced is based on ten years (2008-2017) of satellite derived shortwave incoming solar (SIS) radiation data (horizontal surface). Data aquired and processed as described below.
SIS data ordered and downloaded from CM SAF .
The ordered NetCDF files is delivered as a single TAR (Tape
ARchive) file, which is unpacked using the CM SAF R Toolbox .
Total filesize 935,5 megabytes.
Using the R Toolbox, desired geographical (spatial) coverage is chosen to output 120 pieces of NetCDF files containing the required temporal coverage (ten years and twelve months).
Processing of NetCDF grid data using Python.
Dataset opened using the xarray module .
The SIS parameter extracted and read into an numpy array .
Grid projections defined using pyproj .
2D (longitude/latitude) meshgrid array created using numpy .
Meshgrid transformed into ECEF projection, containg longitude/latitude positions, using pyproj .
Processing of ECEF projection using KDTree from scipy .
Looping through all months and years for the coordinate of interest, to calculate monthly averages.
Returning list of resulting values.
| SISmm200801010000003231000101MA.nc | This sample filename, containing data for January 2008, is one of the 120 NetCDF files that have been processed. |
|---|---|
| cmsafSisReader.py | Python script for processing of the above NetCDF files. |
| Summary of Python source files used for simulations and plots. | ||
|---|---|---|
| Figure | Content | Source files |
| 2.1 | Wavelenght spectrum plot. Data from Matlab Fileexchange . | plotSpectral.py SpectrumAM.xls |
| 2.3 | Ideal PV cell Power & IV-curve plot. | plotIdealCell.py |
| 3.1 | Power consumption timeline plot. | timeline.py |
| 3.2 | Power consumption curve. | kWdischarge24.py |
| 3.4 | Irradiation histogram. | histogramStvg.py |
| 3.5 | Solar irradiation curve, daily average December. | 24irradiation.py |
| 3.7 | PV array output plot, for an average day. | kWcharging24.py |
| 3.8 | PV array output plot, for a "good day". | kWcharging24.py |
| 3.9 | PV array output plot, for a "bad day". | kWcharging24.py |
| 4.1 | Sankey/losses diagram. | sankeyCat1.py |
| 4.2 | Sankey/losses diagram. | sankeyCat2.py |
| 4.3 | Sankey/losses diagram. | sankeyOverall.py |
| 4.4 | 24 hour simulation, at average irradiation. | simulation24h.py |
| 4.5 | 72 hour simulation, at zero irradiation. | simulation72h1.py |
| 4.6 | 72 hour simulation, at "good day" irradiation. | simulation72h2.py |
| 4.8 | Solar irradiation curve, daily average June. | 24irradiationJune.py |